Here, represents the observed values, the predicted values, the regression coefficients, and is the tuning parameter that controls the strength of the penalty.
- When : LASSO regression reduces to OLS, with no penalty applied to the coefficients.
- When increases: The penalty grows, leading to some coefficients shrinking towards zero. This shrinkage property helps eliminate irrelevant features, effectively performing variable selection.
Overfitting Prevention: By regularizing the coefficients, LASSO helps to prevent overfitting, particularly in cases where there are many predictors or multicollinearity exists between variables.
LASSO is often compared with ridge regression, another form of regularization. The key difference lies in the type of penalty applied:
- LASSO uses an -norm penalty, which can shrink coefficients to zero.
- Ridge regression uses an -norm penalty, which shrinks coefficients but doesn't necessarily set them to zero. Ridge is better suited when all predictors are believed to contribute to the outcome, whereas LASSO is ideal for feature selection.
There is also an elastic net model, which combines the penalties of both LASSO and ridge regression, offering a flexible balance between the two approaches.
Applications of LASSO Regression
Finance: LASSO is useful for selecting important variables in financial models, such as those predicting stock prices or default risk. It helps avoid overfitting in models with many correlated predictors.
Genomics: In high-dimensional settings, like genome-wide association studies, LASSO can identify the most relevant genetic variants associated with a particular trait or disease.
Marketing: LASSO helps in understanding which customer characteristics are most predictive of a particular behavior, such as making a purchase or churning from a service.
Healthcare: LASSO can be applied to survival analysis models, where a large number of clinical variables are present, helping to identify the most important risk factors for patient outcomes.
Conclusion
LASSO regression is a robust and versatile tool that strikes a balance between complexity and performance. Its ability to perform automatic feature selection and regularization makes it indispensable in data science, especially in scenarios involving high-dimensional data. Whether in finance, healthcare, or machine learning, LASSO enhances predictive accuracy while maintaining model interpretability, making it a critical method in modern statistical modeling.


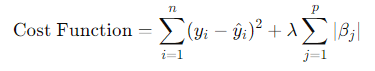



0 Comments